Název etalonu: Státní etalon tíhového zrychlení
Kódové označení: ECM 120-3/08-040
Rok vyhlášení: 2019
Pracoviště: Výzkumný ústav geodetický, topografický a kartografický, v.v.i.,
Ústecká 98, 25066 Zdiby
Garanti: Ing. Vojtech Pálinkáš, Ph.D., Ing. Jakub Kostelecký, Ph.D.
Počet CMC: 2
| Rozsah měření | 9,75 m×s-2 až 9,85 m×s-2 |
| Opakovatelnost měření | 1,2×10-8 m×s-2 |
| Standardní nejistota měření | 2,2×10-8 m×s-2 |
Státní etalon tíhového zrychlení je tvořen dvěma absolutními gravimetry typu FG5 [1] a FG5X [2], které určují zrychlení volného pádu z funkčního vztahu veličin délky a času měřených během volného pádu testovacího tělesa (součástí je koutový odražeč) v prostředí s vysokým stupněm vakua. Volný pád je opakovaně realizován na vzdálenosti 0,2 m / 0,3 m (u FG5 / FG5X) a detekován pomocí laserového interferometru. Ke generovanému interferometrickému signálu s vlnovou délkou určenou kalibrací laseru (jodem stabilizovaný He-Ne laser) je pro tzv. „průchody nulou“ (600 000 / 900 000 vzorků) přiřazen čas (jehož realizaci zajišťuje rubidiový oscilátor). Absolutní tíhová měření jsou tak přímo navázána na jednotky času a vzdálenosti SI prostřednictvím opakovaných kalibrací laseru a rubidiového oscilátoru s relativní nejistotou lepší než 2·10-10.
Určené hodnoty zrychlení volného pádů se korigují na konvenční veličinu tíhového zrychlení, a to zahrnutím okamžitých korekcí z vertikální složky slapového zrychlení, ze změny odstředivého zrychlení vlivem polohy zemských pólů a z proměnlivého zatěžovacího vlivu anomálních atmosférických hmot v souladu s konvencemi IERS [3].
Absolutní balistický gravimetr FG5 č. 215 byl vyhlášen státním etalonem tíhového zrychlení v roce 2008. V roce 2019 proběhla aktualizace státního etalonu, která spočívala jednak ve změně týkající se sestavy a parametrů tohoto gravimetru a jednak v rozšíření etalonu o gravimetr FG5X č. 251. Oba tyto gravimetry byly vyrobeny společností Micro-g LaCoste, v USA a po technologické a metodologické stránce vylepšeny a inovovány na základě intenzivního výzkumu [4-11] realizovaném ve spolupráci ČMI a VÚGTK. Odhaleny, určeny nebo zpřesněny byly významné systematické chyby a příspěvky k nejistotě měření. Gravimetry byly opatřeny novými měřícími systémy a označeny FG5-215/HS5 a FG5X-251/HS5, které aktuálně tvoří státní etalon tíhového zrychlení (viz obr. 1).

Obr. 1. Absolutní gravimetry FG5-215/HS5 (vlevo) a FG5X-251/HS5 (vpravo) tvořící státní etalon tíhového zrychlení.
V roce 2020 byly v KCDB publikovány dvě CMC - pro měření tíhového zrychlení a kalibraci absolutních gravimetrů. Česká republika je první zemí nabízející CMC týkající se kalibrace absolutních gravimetrů.
Vysoká kvalita státního etalonu byla potvrzena již na devíti dosavadních mezinárodních porovnávacích měřeních, viz obr. 2.
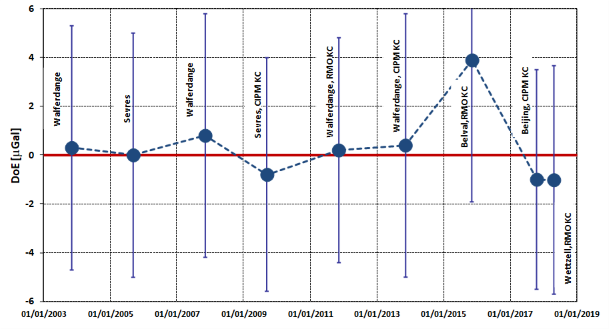
Obr. 2. Odchylky státního etalonu tíhového zrychlení od referenčních hodnot mezinárodních porovnání. Chybové úsečky pro DoE (Degree of Equivalence) představují rozšířenou (k=2) nejistotu tohoto parametru.
Literatura:
- Niebauer T M, Sasagawa G S, Faller J E, Hilt R and Klopping F. A new generation of absolute gravimeters. Metrologia 32:159–180, 1995. https://doi.org/10.1088/0026-1394/32/3/004
- Niebauer T M, Billson R, Ellis B, Mason B van Westrum D and Klopping F. Simultaneous gravity and gradient measurements from a recoil-compensated absolute gravimeter. Metrologia 48:154‑163, 2011. https://doi.org/10.1088/0026-1394/48/3/009
- Petit G, Luzum B. IERS Conventions 2010, IERS Technical Note 36, https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html
- Křen P, Pálinkáš V, Mašika P. On the effect of distortion and dispersion in fringe signal of the FG5 absolute gravimeters. Metrologia 53:27-40, 2016. https://doi.org/10.1088/0026-1394/53/1/27
- Křen P, Pálinkáš V, Mašika P, Vaľko M. FFT swept filtering: a bias-free method for processing fringe signals in absolute gravimeters. Journal of Geodesy 93:219-227, 2018. https://doi.org/10.1007/s00190-018-1154-y
- Křen P, Pálinkáš V, Mašika P, Vaľko M. Effects of impedance mismatch and coaxial cable length on absolute gravimeters. Metrologia 54:161, 2017. https://doi.org/10.1088/1681-7575/aa5ba1. https://doi.org/10.1088/1681-7575/aa5ba1
- Křen P, Pálinkáš V, Mašika P. On the determination of verticality and Eötvös effects in absolute gravimetry. Metrologia 55:451-459, 2018. https://doi.org/10.1088/1681-7575/aac522
- Pálinkáš V, Křen P, Vaľko M and Mašika P. On the determination of vertical gravity gradients by corner-cube absolute gravimeters. Metrologia 56:055006, 2019. https://doi.org/10.1088/1681-7575/ab32fb
- Křen P, Pálinkáš V, Vaľko M, Mašika P. Improved measurement model for FG5/X gravimeters. Measurement 171:108739, 2020. https://doi.org/10.1016/j.measurement.2020.108739
- Křen P and Pálinkáš V. Estimation of the effective wavenumber for a collimated beam in an interferometer, case study for FG5/X absolute gravimeters, Appl. Opt. 61:1811-1817, 2022. https://doi.org/10.1364/AO.451498
- Křen P, Pálinkáš V. Effect of the air-vacuum interface translation on the FG5/X absolute gravimeters. Journal of Geodesy 97:26, 2023. https://doi.org/10.1007/s00190-023-01713-5
